DanW58

float getDiffuseEscapeFractionFromDielectric( float RI ) { float temp = (2.207 * RI) + (RI * RI) - 1.585; return 0.6217 / temp; } float getCosOfAvgReReflectionAngle( float RI ) { return (0.7012 * RI - 0.6062) / (RI - 0.4146); } // getLODbiasFromIR() will be used in ambient lighting. float getLODbiasFromIR( float IR ) //add 5 for 512; add 6 for 1024 cubes { float denominator = IR - 0.3472; float numerator = 0.1342 + (1.293*IR) - (0.123*IR*IR); return numerator / denominator; } void RealFresnel ( vec3 NdotL, vec3 IOR_RGB, out vec3 Frefl, inout vec3 sin_t, inout vec3 cos_t ) { vec3 Z2 = WHITE / IOR_RGB; // Assumes n1 = 1 thus Z1 = 1. vec3 cos_i = NdotL; // assignnment for name's sake vec3 sin_i = sqrt( WHITE - cos_i*cos_i ); sin_t = min(WHITE, sin_i * Z2); // Outputs sin(refraction angle). cos_t = sqrt( WHITE - sin_t*sin_t ); // Outputs cos(refraction angle). vec3 Rs = (Z2*cos_i-cos_t) / (Z2*cos_i+cos_t); vec3 Rp = (Z2*cos_t-cos_i) / (Z2*cos_t+cos_i); Frefl = mix( Rs*Rs, Rp*Rp, 0.5 ); // Outputs reflectivity. } void ReflectedLightPerLightSource //excludes refract out; includes Phong ( float raydotnormal, float halfdotnormal, float eyedotlight, vec3 srcRGBlight, vec3 RefractiveIndex, vec3 specColRGB, float MatSpecPower, vec3 MatDiffuseRGB, out vec3 specularRGBlight, out vec3 diffuseRGBlight ) { //Phong related things: float sinAngularRng = pow(0.5, (1.0 / SpecPower)); float PhongDispersionFactor = 0.5 / ( 1.0 - sinAngularRng ); float NdotLcorrection = sqrt(1-sinAngularRng*sinAngularRng))*(eyedotlight); float newNdotL = clamp( raydotnormal + NdotLcorrection, 0.0, 1.0 ); float Phong = PhongDispersionFactor * pow(halfdotnormal, SpecPower) * (newNdotL+0.1) / (raydotnormal+0.1); //Fresnel related things: vec3 FReflectivityRGB; vec3 sinRefrAngle; vec3 cosRefrAngle; RealFresnel( vec3(newNdotL), RefractiveIndex, ReflectivityRGB, sinRefrAngle, cosRefrAngle ); vec3 FRefractivityRGB = WHITE-FReflectivityRGB; vec3 EscapeFraction = getDiffuseEscapeFractionFromDielectric( RefractiveIndex ); float cosAvgReflAngle = getCosOfAvgReReflectionAngle( RefractiveIndex ); //specular: vec3 RRratio = FReflectivityRGB * specColRGB; vec3 dead_light = FRefractivityRGB / ( WHITE - RRratio ); //simplification for infinite specular bounces: vec3 nbouncesRGB = ((WHITE/FReflectivityRGB)-WHITE) * dead_light; vec3 specularFactorRGB = FReflectivityRGB + nbouncesRGB/FRefractivityRGB; //(1) specularRGBlight = Phong * srcRGBlight * specularFactorRGB; //diffuse: //First refraction and diffuse bounce vec3 temp3 = /*(WHITE-ReflectivityRGB)*/ * cosRefrAngle * MatDiffuseRGB; //(2) //And computing the first diffuse escape: temp3 *= EscapeFraction; //simplification for infinite diffuse bounces: vec3 r = (WHITE-EscapeFraction) * vec3(cosAvgReflAngle) * MatDiffuseRGB; vec3 diffuseFactorRGB = temp3 / (WHITE-r); diffuseRGBlight = srcRGBlight * diffuseFactorRGB; } //(1) Switching policy to report total light going up un-modulated by emergent //refraction, as Fresnel based on View dot Normal is better for that. This is //the reason for dividing nbouncesRGB by FRefractivityRGB. //(2) Switching policy to report total light going up, instead of total light //emerging, and letting the viewer modulate by Fresnel refract from eye-view; //thus, diffuseFactorRGB now represents a value slightly > normal-aligned light.

Wait! What would be so wrong if we used the same diffuse correction factor for specularity? If we can't see some part of the terrain due to bump over-shadowing, it's no different whether the bounce is diffuse or specular. Let's try it and see what happens: We were talking about subtracting the sine of the mean roughness angle from NdotL. We'd want to do that when the sun is away from us, like on the other side of the object. When the sun is on our side of the object, such as behind us, we'd probably want to add the roughness angle to NdotL. Thus, NdotL += sqrt(1-0.5^(2/n))*(EdotL); Does that express what we just discussed? The term sqrt(1-0.5^(2/n)) is what we worked out earlier to be the sine of the mean angularity as a function of n, the specular power. EdotL is the dot product of view vector and light vector, which we hereby allow to span from -1.0 to +1.0. If the sun is behind us, EdotL is about +1, and so we add the sine of the roughness to NdotL. If the sun is on the other side of our object, EdotL is negative, towards -1.0, and so we are subtracting sine of angularity from NdotL. In both cases we need to clamp NdotL to 0.0~1.0 range after the addition and subtraction. If now we divide the new NdotL by the old NdotL, we get a "correction factor applied", which we can then turn around and apply to specularity as well. Should I say "BINGO!" ? I'm not sure; I think I'll leave the cork in the champagne bottle undisturbed for now. Tentatively updating the code: float getPhongFactor ( float lightdotnormal, float eyedotlight, float halfdotnormal, float SpecPower out float NdotLcorrection; ) { float FunnyNumber = pow(0.5, (1.0 / SpecPower)); float PhongDispersionFactor = 0.5 / ( 1.0 - FunnyNumber ); float sinAngularRng = sqrt(1-FunnyNumber*FunnyNumber))*(eyedotlight); float correctionPolarity = eyedotlight; float newNdotL = clamp(lightdotnormal + sinAngularRng*correctionPolarity, 0.0, 1.0); NdotLcorrection = (newNdotL+0.1) / (lightdotnormal+0.1); return PhongDispersionFactor * NdotLcorrection * pow(halfdotnormal, SpecPower); } I don't like it, at this point. I don't like the fact I'm having to hack NdotLcorrection to avoid division by zero. I don't like that we compute the NdotL correction here, in specular, and output the correction for the diffuse routine to pickup. I have a lot of bad feelings about this, but can't put my finger on the culprit, so I let it stand as is for now.

Let's see: NdotL is the cosine of the sun's angle to the normal. It is also the sine of the sun's angle to the un-roughened surface. If the sun's angle to the surface is small, the sine is roughly same value as the angle. If the sine of the sun's angle to the surface is comparable to the sine of mean surface angularity, the effect is the same as if the sun had an angle to surface that much lower. So we could just subtract the sine of the surface mean angle from the sun's NdotL, and that would have a similar effect to rotating the sun by the same angle. Right? We don't even have to touch vectors! Right? ... Except! This is a diffuse lighting solution; not specular. But I think this holds true for diffuse, so let's not throw it away; I think this is a winner; and we'll come back to it and refine it. For specular lighting, we use the normal dot the half-vector (the vector between the sun and the eye), so it's not so easy yet. Truly, the half vector isn't very useful here; is it? Hmmm...

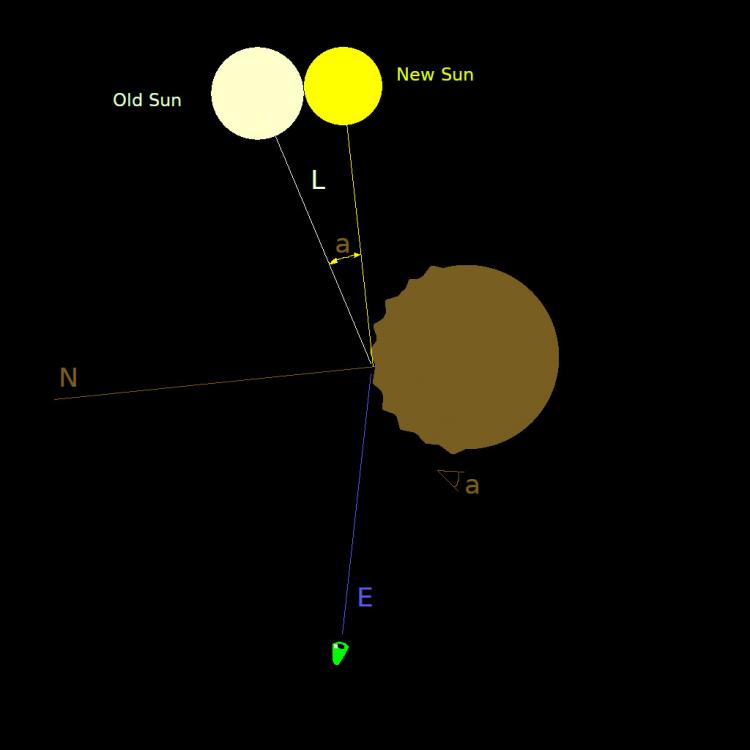
This is what I'm talking about: The effect of the sun's shading on an angular surface is the same as if the surface was flat but the sun was angled away from us by an angle equal to the very surface angularity. The normal here is irrelevant, I think... I now have to figure out how to implement this light vector rotation.

Holly cow! I just remembered that 20 years ago I resolved this very problem, and it's just starting to come back how I did it ... It was in the context of planet rendering. Just a very vague memory ... I ended up scaling the angle of the sun as a function of roughness. A very angular surface caused the light source to move towards its horizon, or even fall behind it. Of course I wasn't moving the Sun itself; --not even the virtual one--; I mean for that pixel I was rendering, surface's mean angularity got added to the light vector's angle to the eye vector, I think it was, --just inside my Phong function; not in general. It was a very simple trick and worked like a charm. The beauty of it was the simplicity of the solution. Everybody else were doing heavy computations to modify Phong; I just found that moving the light did a better job. And I seem to remember this was also helping with adjusting diffuse lighting with surface roughness. Now if I can just summon the memory of the details ...

Okay, I'm starting to see the light at the end of the tunnel... Okay, we are looking at a sphere. Our eyes are fixated on a point near the left horizon on the sphere. Now let's play with the Sun's position: If it is right behind us, it makes the bumpiness near the horizon of the sphere light up like phosphoro-cheese-cake. If it is right on the other side, or barely to the left of the sphere's horizon, it makes the far-side of the bumps light up, but our side of them is in darkness; so the net result is darkening. However, the effect is not symmetrical. Or, is it? I think that from the Sun being behind us, to it being say 45 degrees between behind us and to the left, there is not much change on bump illumination. I don't think bump self-shadowing plays any role in this case. I'm starting to forget we are talking about specular light here; I was slipping into a diffuse mindset. GAD this problem is hard!

Could it simply be that this should be a function of the light vector, and NOT the eye vector? EDIT: Nope.

No; that's not correct. I was only considering in the case of the light being on the other side, litting the back-faces. Should the light direction figure into this? Well, if the light is behind us, roughness at shallow angles will make the surface look MORE bright, not less; so yes, the light direction is important. In fact, this is why the full moon shades like a flat disk of cheese: It's the fact that it's not terribly smooth. Think, think, think ...

Indeed. SpotRadius = arccos( 0.5^(1/n) ) In other words, cos(radius) = 0.5^(1/specpower); sin(x) = sqrt(1-cos(x)^2), so sin(x) = sqrt(1-0.5^(2/n)) Our dimming factor could be computed as PhongDF = clamp( dot(eyeVec, normal) / sqrt(1.0-pow(0.5, 2.0/specpower)); Thus, our full Pong function could look like this: float getPhongFactor(vec3 eyedotnormal, vec3 halfdotnormal, float SpecPower) { float FunnyNumber = pow(0.5, (1.0 / SpecPower)); float PhongDispersionFactor = 0.5 / ( 1.0 - FunnyNumber ); float PhongSelfOccludFactor = clamp(eyedotnormal / sqrt(1.0-FunnyNumber*FunnyNumber), 0.0, 1.0); float PhongFactor = PhongDispersionFactor * PhongSelfOccludFactor * pow(halfdotnormal, SpecPower); }

Phong sucks! Yes, I've said it. The way it is traditionally used in shaders is particularly retarded. People forget that the lower the spec power, and the wider the reflection spots, the more dispersed the reflection is, and therefore the less bright each pixel looks. The total light is invariant with spec power, but the per-pixel light needs to be adjusted for spread. But article after article on Phong shading fails to mention this. That's why I have a PhongDispersionFactor variable in the code of the last post. But there's more to the crappiness of Phong; and no; it's not that pow(dot,specpwr) is not physics based; it is actually quite close to actual optics ... up to a point ... and that point is where the surface bumps start shadowing each other. This point, in other words, is where the theoretical micro-bumpiness of the surface, at a given view angle, would start generating back-facing faces, if it was a mesh-modifier. So, if you are looking at a sphere, with a light almost 180 degrees on the other side, plain Phong will give you a very bright color no matter the roughness of the surface; but this is wrong, because a rough surface would have a lot of points facing away and lit, and many points facing towards us, but in shadow. There needs to be a dimming factor to account for this. The more shallow the angle, and lower the specpower, the more dimming. No; NOT a dimming: rather a function that overshadows phong, such that the lower of the two values is used. It should make a sharp corner where it undercuts phong, precisely at the point where the implied bumpiness starts generating back-facing areas in the surface. But how can we calculate where this point is, and what function to use to undercut Phong with? Okay, let's consider the strange, unnatural, yet simplest case of specpower = 1.0. As we saw in the first post of this thread, the spread of light on a specular sphere with specpower = 1.0 is differently aligned but of equal spread as the same sphere's white diffuse equivalent. A white diffuse sphere reflects at 1/2 strength at 60 degrees to the light source. A specular sphere with specpower = 1.0 reflects at 1/2 strength at 60 degrees from the half-vector. Not quite isotropically, but basically ... Actually, it is hard to visualize the bumps that would cause 50% reflectivity towards us at 60 degrees to the half-vector. I've seen papers on this very subject before, and the authors always model the problem as a surface full of random flat faces, and now I understand why. NO surface will reflect any light towards you unless it is perfectly aligned and then it sends you ALL the light, unless that surface itself has a specpower. The only way to even begin to analyze this you have to make surface detail into a fractal. Is there a better way to tackle this problem? I know, for each specular power, what the blur cone's half angle and solid angle are. Does this help? The radius of the blur cone is basically the mean deviation from the normal ... actually it is twice the mean deviation, I think... What if we simplify that to say that surface normals span +/- cone_radius/2 in U and V? We can figure the exact absolute numbers later; a rough approximation will be orders of magnitude better looking than nothing. Or even simpler than that, what if we say that IF the view-vector's angle to the surface is less than 1/2 the blur radius, we start dimming the light? Comparing angles, as usual, would involve expensive calls to arccos(); we can simply compare cos or compare sin. Of the two, sine makes a lot more sense, as it is close to the angle for small angles, which are our chief concern. The sine of the angle to the surface is actually the cos of the angle to the normal, so we can compute dot(eyevec,normal) and rename it "sinofangletosurface". The sine of the radius of our blur-cone equivalent to our material spec power may involve taking a square root, as I think that what we have is the cosine of it; let me check ...

Revised code to include Phong: float getDiffuseEscapeFractionFromDielectric( float RI ) { float temp = (2.207 * RI) + (RI * RI) - 1.585; return 0.6217 / temp; } float getCosOfAvgReReflectionAngle( float RI ) { return (0.7012 * RI - 0.6062) / (RI - 0.4146); } // getLODbiasFromIR() will be used in ambient lighting. float getLODbiasFromIR( float IR ) //add 5 for 512; add 6 for 1024 cubes { float denominator = IR - 0.3472; float numerator = 0.1342 + (1.293*IR) - (0.123*IR*IR); return numerator / denominator; } void RealFresnel ( vec3 NdotL, vec3 IOR_RGB, out vec3 Frefl, inout vec3 sin_t, inout vec3 cos_t ) { vec3 Z2 = WHITE / IOR_RGB; // Assumes n1 = 1 thus Z1 = 1. vec3 cos_i = NdotL; // assignnment for name's sake vec3 sin_i = sqrt( WHITE - cos_i*cos_i ); sin_t = min(WHITE, sin_i * Z2); // Outputs sin(refraction angle). cos_t = sqrt( WHITE - sin_t*sin_t ); // Outputs cos(refraction angle). vec3 Rs = (Z2*cos_i-cos_t) / (Z2*cos_i+cos_t); vec3 Rp = (Z2*cos_t-cos_i) / (Z2*cos_t+cos_i); Frefl = mix( Rs*Rs, Rp*Rp, 0.5 ); // Outputs reflectivity. } void ReflectedLightPerLightSource //excludes Fresnel refract out; includes Phong ( float raydotnormal, float halfdotnormal, vec3 srcColorRGBlight, vec3 RefractiveIndex, vec3 specColRGB, float MatSpecPower, vec3 MatDiffuseRGB, out vec3 specularRGBlight, out vec3 diffuseRGBlight ) { vec3 FReflectivityRGB; vec3 sinRefrAngle; vec3 cosRefrAngle; RealFresnel( vec3(raydotnormal), RefractiveIndex, ReflectivityRGB, sinRefrAngle, cosRefrAngle ); vec3 FRefractivityRGB = WHITE-FReflectivityRGB; vec3 EscapeFraction = getDiffuseEscapeFractionFromDielectric( RefractiveIndex ); float cosAvgReflAngle = getCosOfAvgReReflectionAngle( RefractiveIndex ); float PhongDispersionFactor = 0.5 / ( 1.0 - pow(0.5, (1.0 / MatSpecPower)) ); float PhongFactor = PhongDispersionFactor * pow( halfdotnormal, MatSpecPower ); //specular: vec3 RRratio = FReflectivityRGB * specColRGB; vec3 dead_light = FRefractivityRGB / ( WHITE - RRratio ); //simplification for infinite specular bounces: vec3 nbouncesRGB = ((WHITE/FReflectivityRGB)-WHITE) * dead_light; vec3 specularFactorRGB = FReflectivityRGB + nbouncesRGB/FRefractivityRGB; //(1) specularRGBlight = PhongFactor * srcColorRGBlight * specularFactorRGB; //diffuse: //First refraction and diffuse bounce vec3 temp3 = /*(WHITE-ReflectivityRGB)*/ * cosRefrAngle * MatDiffuseRGB; //(2) //And computing the first diffuse escape: temp3 *= EscapeFraction; //simplification for infinite diffuse bounces: vec3 r = (WHITE-EscapeFraction) * vec3(cosAvgReflAngle) * MatDiffuseRGB; vec3 diffuseFactorRGB = temp3 / (WHITE-r); diffuseRGBlight = srcRGBlight * diffuseFactorRGB; } //(1) Switching policy to report total light going up un-modulated by emergent //refraction, as Fresnel based on View dot Normal is better for that. This is //the reason for dividing nbouncesRGB by FRefractivityRGB. //(2) Switching policy to report total light going up, instead of total light //emerging, and letting the viewer modulate by Fresnel refract from eye-view; //thus, diffuseFactorRGB now represents a value slightly > normal-aligned light. Of note: dot product of normal and half-vector is now added to the inputs; also material smoothness (specular power), and so now emerging specular light is already Phong-modulated. Something needs to be said about the new shaders: We need a comprehensive way to package the uniforms and varyings. SunLight, SunDir, and HalfVec are all PER LIGHT SOURCE items. Also, the getShadow() and getShadowOverTerrain() functions need to have a light source identifier as argument. Even if 0ad will never have more than one Sun, who knows what this engine could be used for in the future? A Trisolarian civ mod would be in deep trouble right now.

So, as I was saying, "...next stage in the pipeline would be the eyeVector Fresnel refraction modulation and Fresnel reflection modulated environment mapping, plus ambient. This next stage would also compute Phong." Oh, no! Another HUGE mistake ... Phong has to be computed per-light. So, our previous routine HAS to include Phong. Well, better to discover mistakes at this stage than to discover them at revision 42...

I've just decided against testing this by itself. It is too difficult, given that nothing like this function exists in any of the current shaders, and therefore the interfaces are not there to plug this in. To plug this in I need to modify the existing code to conform to this model. But what is easier to do? Modify old code?, or write new code? Definitely the latter; so might as well complete the pipeline here, and test the whole thing. This function gives us reflectivity per light, excluding emerging fresnel modulation. The next stage in the pipeline would be the eyeVector Fresnel refraction modulation and Fresnel reflelction modulated environment mapping plus ambient. This next stage would also compute Phong. Darn! I just realized I made a policy mistake in NOT including sunColor (or light color/intensity) as an input: This is an error because if we have more than one light in a scene (even if this may never be the case with 0ad), the fact remains that I cannot plug in the light colors AFTER the total reflectivities from all the lights are added. At each light I have a unique and final opportunity to plug-in the color of it. The code change is minor, but the conceptual perspective shift is considerable. So now I have one more input argument: sunColorRGBlight, and my outputs are measures of LIGHT, not of reflectivity. Updated code: float getDiffuseEscapeFractionFromDielectric( float RI ) { float temp = (2.207 * RI) + (RI * RI) - 1.585; return 0.6217 / temp; } float getCosOfAvgReReflectionAngle( float RI ) { return (0.7012 * RI - 0.6062) / (RI - 0.4146); } // getLODbiasFromIR() will be used in ambient lighting. float getLODbiasFromIR( float IR ) //add 5 for 512; add 6 for 1024 cubes { float denominator = IR - 0.3472; float numerator = 0.1342 + (1.293*IR) - (0.123*IR*IR); return numerator / denominator; } void RealFresnel ( vec3 NdotL, vec3 IOR_RGB, out vec3 Frefl, inout vec3 sin_t, inout vec3 cos_t ) { vec3 Z2 = WHITE / IOR_RGB; // Assumes n1 = 1 thus Z1 = 1. vec3 cos_i = NdotL; // assignnment for name's sake vec3 sin_i = sqrt( WHITE - cos_i*cos_i ); sin_t = min(WHITE, sin_i * Z2); // Outputs sin(refraction angle). cos_t = sqrt( WHITE - sin_t*sin_t ); // Outputs cos(refraction angle). vec3 Rs = (Z2*cos_i-cos_t) / (Z2*cos_i+cos_t); vec3 Rp = (Z2*cos_t-cos_i) / (Z2*cos_t+cos_i); Frefl = mix( Rs*Rs, Rp*Rp, 0.5 ); // Outputs reflectivity. } void ReflectedLightPerLightSource //excludes Fresnel refract out modulation ( float raydotnormal, vec3 srcColorRGBlight, vec3 RefractiveIndex, vec3 specColRGB, vec3 MatDiffuseRGB, out vec3 specularRGBlight, out vec3 diffuseRGBlight ) { vec3 FReflectivityRGB; vec3 sinRefrAngle; vec3 cosRefrAngle; RealFresnel( vec3(raydotnormal), RefractiveIndex, ReflectivityRGB, sinRefrAngle, cosRefrAngle ); vec3 FRefractivityRGB = WHITE-FReflectivityRGB; vec3 EscapeFraction = getDiffuseEscapeFractionFromDielectric( RefractiveIndex ); float cosAvgReflAngle = getCosOfAvgReReflectionAngle( RefractiveIndex ); //specular: vec3 RRratio = FReflectivityRGB * specColRGB; vec3 dead_light = FRefractivityRGB / ( WHITE - RRratio ); //simplification for infinite specular bounces: vec3 nbouncesRGB = ((WHITE/FReflectivityRGB)-WHITE) * dead_light; vec3 specularFactorRGB = FReflectivityRGB + nbouncesRGB/FRefractivityRGB; //(1) specularRGBlight = srcColorRGBlight * specularFactorRGB; //diffuse: //First refraction and diffuse bounce vec3 temp3 = /*(WHITE-ReflectivityRGB)*/ * cosRefrAngle * MatDiffuseRGB; //(2) //And computing the first diffuse escape: temp3 *= EscapeFraction; //simplification for infinite diffuse bounces: vec3 r = (WHITE-EscapeFraction) * vec3(cosAvgReflAngle) * MatDiffuseRGB; vec3 diffuseFactorRGB = temp3 / (WHITE-r); diffuseRGBlight = srcRGBlight * diffuseFactorRGB; } //(1) Switching policy to report total light going up un-modulated by emergent //refraction, as Fresnel based on View dot Normal is better for that. This is //the reason for dividing nbouncesRGB by FRefractivityRGB. //(2) Switching policy to report total light going up, instead of total light //emerging, and letting the viewer modulate by Fresnel refract from eye-view; //thus, diffuseFactorRGB now represents a value slightly > normal-aligned light. Done! Of note: Main function changed name; it has a new input "srcRGBlight" (a better name than "sunColor"), and the two outputs of the function changed names from "factor"s to denote light amounts.

Coffee is having its desired effect. I just realized that indeed, the diffuse light coming out of a dielectric absolutely HAS to be modulated by Fresnel refractivity computed on the view vector. However: The emerging light figure that our unified formula yields is for total light going out. There are two ways we could proceed with this modulation: Compute a modulation that goes above and below 1.0 as to be neutral on a spherical average. Compute a standard refractive modulation, but have our universal formula scale the light back up so that it represents the maximum light coming out along the normal. Of the two, the second option is the easiest, not only because our Fresnel routine already computes standard Fresnel refractive factor, but also because our unified formula KNOWS what the peak light is; namely the light exploding up after each diffuse bounce, before subtracting the light reflected back down! In other words, all we have to do is throw away the total diffuse light emerging output; and instead have an output of total light trying to emerge, and let the viewer figure out how much of it is visible based on Fresnel refraction from the eye of the beholder. BINGO! Ah, wait a minute! What about metallic specular multi-bounce emerging light? Does that not need a similar treatment? Let's think ... At first sight, it would appear not, since, by definition, Fresnel based on eye-view and Fresnel based on the light source are about the same if we are seeing a reflection. However, on second thought, this would be a terrible mistake: It would make the two outputs of this function inconsistent: the specularity output including emerging refractive modulation, but the diffuse output not doing so. BAD!!! It also ignores materials with very low shininess where the sun and view Fresnel factors may not be the same at all and still be pushing light into the eye. And last but not least it ignores the fact that modulating by eye-view Fresnel has almost zero cost; since we HAVE to compute such Fresnel for environment mapping anyways. So, yes, BOTH specular and diffuse are now going to report total light trying to emerge from the dielectric. The eye of the beholder shall later decide how much of it does emerge towards it. Updated code: float getDiffuseEscapeFractionFromDielectric( float RI ) { float temp = (2.207 * RI) + (RI * RI) - 1.585; return 0.6217 / temp; } float getCosOfAvgReReflectionAngle( float RI ) { return (0.7012 * RI - 0.6062) / (RI - 0.4146); } // getLODbiasFromIR() will be used in ambient lighting. float getLODbiasFromIR( float IR ) //add 5 for 512; add 6 for 1024 cubes { float denominator = IR - 0.3472; float numerator = 0.1342 + (1.293*IR) - (0.123*IR*IR); return numerator / denominator; } void RealFresnel ( vec3 NdotL, vec3 IOR_RGB, out vec3 Frefl, inout vec3 sin_t, inout vec3 cos_t ) { vec3 Z2 = WHITE / IOR_RGB; // Assumes n1 = 1 thus Z1 = 1. vec3 cos_i = NdotL; // assignnment for name's sake vec3 sin_i = sqrt( WHITE - cos_i*cos_i ); sin_t = min(WHITE, sin_i * Z2); // Outputs sin(refraction angle). cos_t = sqrt( WHITE - sin_t*sin_t ); // Outputs cos(refraction angle). vec3 Rs = (Z2*cos_i-cos_t) / (Z2*cos_i+cos_t); vec3 Rp = (Z2*cos_t-cos_i) / (Z2*cos_t+cos_i); Frefl = mix( Rs*Rs, Rp*Rp, 0.5 ); // Outputs reflectivity. } void Reflectivity ( float raydotnormal, vec3 RefractiveIndex, vec3 specColRGB, vec3 MatDiffuseRGB, out vec3 specularFactorRGB, out vec3 diffuseFactorRGB ) { vec3 FReflectivityRGB; vec3 sinRefrAngle; vec3 cosRefrAngle; RealFresnel( vec3(raydotnormal), RefractiveIndex, ReflectivityRGB, sinRefrAngle, cosRefrAngle ); vec3 FRefractivityRGB = WHITE-FReflectivityRGB; vec3 EscapeFraction = getDiffuseEscapeFractionFromDielectric( RefractiveIndex ); float cosAvgReflAngle = getCosOfAvgReReflectionAngle( RefractiveIndex ); //specular: vec3 RRratio = FReflectivityRGB * specColRGB; vec3 dead_light = FRefractivityRGB / ( WHITE - RRratio ); //simplification for infinite specular bounces: vec3 nbouncesRGB = ((WHITE/FReflectivityRGB)-WHITE) * dead_light; specularFactorRGB = FReflectivityRGB + nbouncesRGB/FRefractivityRGB; //(1) //diffuse: //First refraction and diffuse bounce vec3 temp3 = /*(WHITE-ReflectivityRGB)*/ * cosRefrAngle * MatDiffuseRGB; //(2) //And computing the first diffuse escape: temp3 *= EscapeFraction; //simplification for infinite diffuse bounces: vec3 r = (WHITE-EscapeFraction) * vec3(cosAvgReflAngle) * MatDiffuseRGB; diffuseFactorRGB = temp3 / (WHITE-r); } //(1) Switching policy to report total light going up un-modulated by emergent //refraction, as Fresnel based on View dot Normal is better for that. This is //the reason for dividing nbouncesRGB by FRefractivityRGB. //(2) Switching policy to report total light going up, instead of total light //emerging, and letting the viewer modulate by Fresnel refract from eye-view; //thus, diffuseFactorRGB now represents a value slightly > normal-aligned light.

I knew this was a tough one; I tried hard to get anything to work; infinite thanks. And it works perfectly. float getLODbiasFromIR( float IR ) //add 5 for 512; add 6 for 1024 cubes { float denominator = IR - 0.3472; float numerator = 0.1342 + (1.293*IR) - (0.123*IR*IR); return numerator / denominator; } One subject not dealt with yet is rougness/smoothness, improving the Phong model, and how spec power and Fresnel combine. But I'm just waking up for now. EDIT: Spreadsheet updated: EDIT2: LOL, when someone complains "it's too dark", "it's too bright", ... I'll just ask them "would you care to review the math?" FresnelTable.ods